Computational Art: No 1

Dan Gray

2017/11/06

Summary

This post is inspired by the work of Antonio Sánchez Chinchón, and his original post on Clifford Attractors.

In a nutshell I wanted to replicate his approach whilst making three clear deviations, namely:

  1. using base R instead of optimised Rcpp (C++) code for the computation
  2. randomise the parameters to create an “infinite” number of outcomes
  3. save this output into many tiles

Background and Theory

Clifford attractors are infinite attractors described by 4 parameters (a, b, c, d) and 2 equations. Starting with an initial value for two values X and Y one computes the next starting point-pair. Thus the computation is sequential and this means generating point-pairs or trajectories from the previous outcome.

I chose a basic looping approach to fill a data frame of 1 million point-pairs.

The approach has several steps:

  1. Define the global parameters (how many points to generate, how many iterations to run)

  2. Wrap the below steps in a loop
    1. Generate random parameters over a given domain using runif
    2. Create holder vector for the results
    3. Define the attractors and compute the first point

Intialisation

library(scales)

# set global paramaters
xs=runif(1000000) # vector of length(~4Mb for 5x10^5)
gens=seq(1:12) # number (n) of images to generate

Main Loop

# main loop
for (j in 1:length(gens)){

# model parameters (~ 4:1 generation ratio!)
a = runif(1,min=1,max=2)*-1
b = runif(1,min=1,max=2)*-1
c = runif(1,min=1,max=2)*-1
d = runif(1,min=1,max=2)*-1

# make holder vectors
res1 <- numeric(length(xs)+1)
res2 <- numeric(length(xs)+1)

# define clifford attractors eq at X=0, Y=0
res1[1] <- sin(a)-c*cos(a)
res2[1] <- sin(b)-d*cos(b)

# sequential trajectories derived from previous values
for (i in seq_along(xs)) {
  res1[i+1] <- sin(a*res2[i])+c*cos(a*res1[i])
  res2[i+1] <- sin(b*res1[i])+d*cos(b*res2[i])
  }

}

Plot a Single Example

# single case plot
plot(res1,res2,type="p",pch=16,asp=1,
     cex=0.01,col=alpha("black",0.02),xlim=c(-3,3),
     ylim=c(-3,3),axes=FALSE,xlab="",ylab="")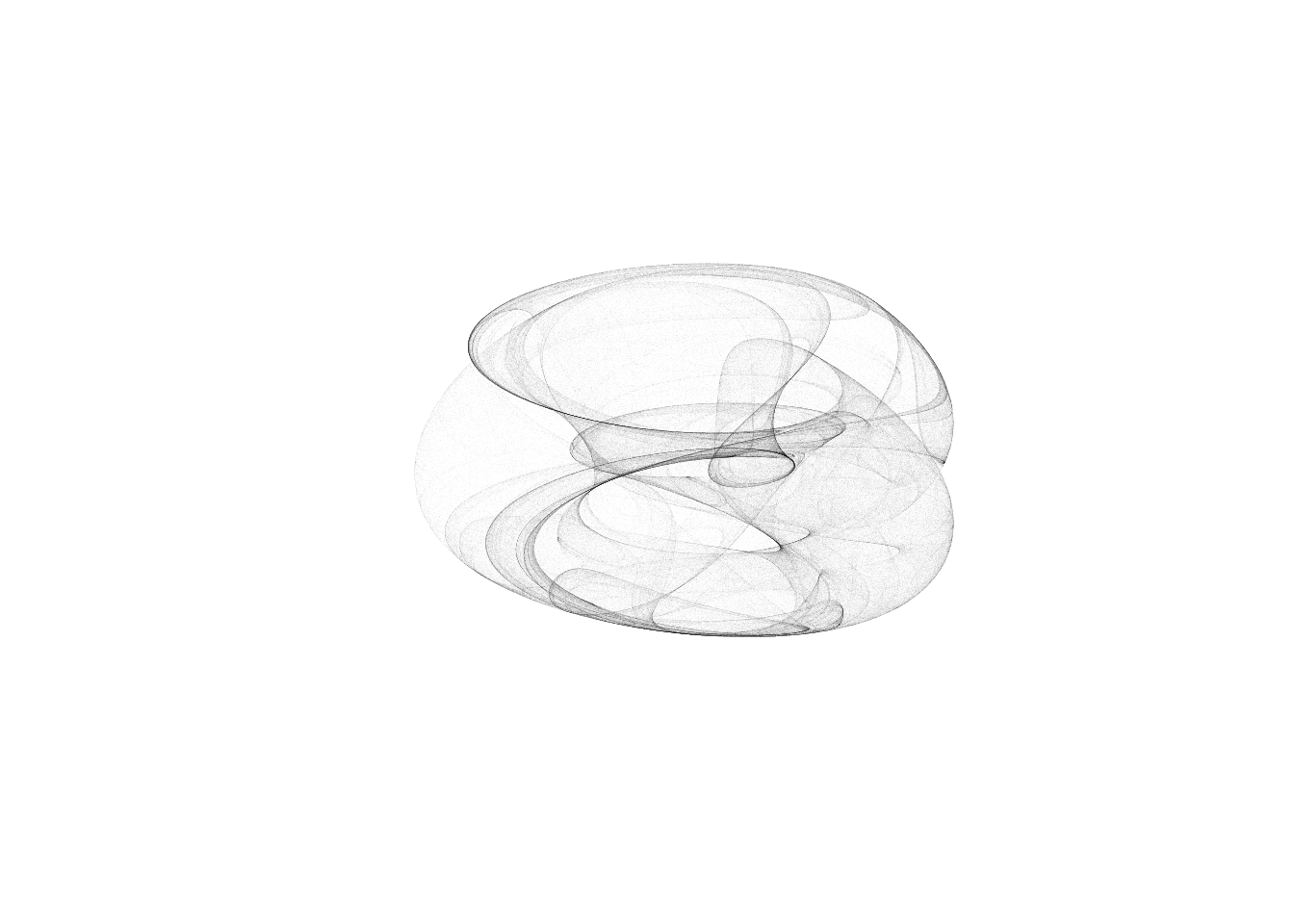

Iterate N Times as Desired

Substitute and replace the single case plot call above with this code block to generate, and save n number of iterations.

# generate distinct labels for output
lab <- paste0(sample(letters,5),collapse="")

# multiple case plotting
png(paste0("imgs/",lab,".png"),units="px", width=2000, height=2000,res=300)
plot(res1,res2,type="p",pch=16,asp=1,
     cex=0.01,col=alpha("black",0.02),xlim=c(-3,3),
     ylim=c(-3,3),axes=FALSE,xlab="",ylab="")
dev.off()