Summary
In a previous exercise I examined how well simple “chance-based” games represent the creation of wealth disparity.
Here I continue on this exercise by using a so-called Kinetic-Exchange model to approximate exchange in an economic system.
The Model Description
The model consists of:
- X agents, each given a starting value V
- N interactions
- in each round, two agents are selected at random, one is assigned a “winner”, the other a “loser”
- a sum, S is transferred from “loser” to the “winner”
- this sum is drawn from the uniform distribution (0, to the mean value of all agents)
- this amount is transferred only if the “loser” has the available funds, otherwise both players wealth is left unaltered
This procedure continues until the selected interaction-period is complete.
Implementation
My implementation consists of:
a model function (captures the exchange mechanism),
a stepper function which;
- defines the starting parameters (number of players, interaction length, taxation)
- steps through all the interactions (using a loop-structure)
- creates a diagnostic of the inequality trend over time
- A replication mechanism using the function
replicate
One fundamental approach struck me as being relevant for this (and other) simulation schemes.
As the interaction scheme is driven by random processes each run will return unique paths of interaction
To understand the bounds of the interactions, and the parameters that drive them I needed to be able to repeat (replicate) simulations with given parameter sets.
R provides such a mechanism, or rather the wrapper for this with the replicate function. Simply wrap your code in a function, and pass this function to replicate with the given number of repeats.1
Simulation Runs: No Taxation vs. Wealth Redistribution Schemes
Here is the kinetic-exchange function:
library(tidyverse)
# create energy-simulation function
energies <- function(x){
Wpos <- sample(x[,1],1)
Lpos <- sample(x[,1],1)
transfer <- runif(n = 1,min=0,max=mean(x[,2]))
if (x[Lpos,2] > transfer) {
x[Wpos,2] <- x[Wpos,2]+transfer
x[Lpos,2] <- x[Lpos,2]-transfer
x[Wpos,3] <- x[Wpos,3]+1
x[Lpos,3] <- x[Lpos,3]+1
} else {
x[Wpos,2] <-x[Wpos,2]
x[Lpos,2] <-x[Lpos,2]
x[Wpos,3] <- x[Wpos,3]+1
x[Lpos,3] <- x[Lpos,3]+1
}
vals <- x[,1:3]
}The stepper function creates the initial data-set using given arguments from the function call itself.
If a wealth redistribution scheme is applied (where rate !=0), then an interval is constructed over which all agents will be taxed at fixed rate, wF. The sum of all taxes will then be evenly redistributed over all agents (reducing the inequality gap).
A logbook of exchanges is prepared (transactions) which captures the values of all players for every iteration (a matrix of size nsteps * agents).
A stream of the total taxed amount, and individual returns is optionally outputted to the terminal.
Within the loop itself the transactions are recorded, and a diagnostic measure of wealth inequality comparing the “Top 1% of earners” and the “Bottom 50%” is computed and returned as the default object of the function
# create stepper function
stepper <- function(nsteps=10000,agents=200,rate=0.1,wF=0.025) {
# build intial game
dat <- matrix(c(1:agents,rep(100,agents),
rep(0,agents)),nrow=agents)
# define redistribution rates/intervals
rDis <- round(nsteps*rate,-1)
# setup for NULL taxation
if (rDis==0){
rInt <-seq(1,nsteps,nsteps)
wF <- 0
} else {
rInt <- seq(rDis,nsteps,rDis)
}
# define ranking system
rank_01 <- agents/100
rank_50 <- agents - (agents/2)+1
# prepare logbook of transactions
transactions <- matrix(ncol=nsteps,nrow=agents)
# prepare diagnostics
diagnostics <- matrix(ncol=4,nrow=nsteps)
for (i in seq_len(nsteps)){
if (i %in% rInt) {
dat <- energies(dat)
# Redistribution Scheme
totTaxes <-sum(dat[,2]*wF)
indSplits <- totTaxes/agents
#print(paste0(totTaxes,": All"))
#print(paste0(indSplits,": Split"))
dat[,2] <- dat[,2]+indSplits
# extract transaction and counter
trn <-dat[,2]
cnt <-dat[,3]
# sorting of results for diagnostics
sorts <- dat[order(dat[,2],decreasing=TRUE),]
pos01_unit <- sorts[1,1]
pos01_val <- sorts[1,2]
pos50_val <-sum(sorts[rank_50:agents,2])
diagnostics[i,1] <-pos01_unit
diagnostics[i,2] <-pos01_val
diagnostics[i,3] <-pos50_val
diagnostics[i,4] <-round((pos01_val/pos50_val)*100,1)
# pass per-round balances to logbook
transactions[,i]<-trn
} else {
# pass function results back to DF
dat <-energies(dat)
# extract transaction and counter
trn <-dat[,2]
cnt <-dat[,3]
# sorting of results for diagnostics
sorts <- dat[order(dat[,2],decreasing=TRUE),]
pos01_unit <- sorts[1,1]
pos01_val <- sorts[1,2]
pos50_val <-sum(sorts[rank_50:agents,2])
diagnostics[i,1] <-pos01_unit
diagnostics[i,2] <-pos01_val
diagnostics[i,3] <-pos50_val
diagnostics[i,4] <-round((pos01_val/pos50_val)*100,1)
# pass per-round balances to logbook
transactions[,i]<-trn
}
}
# return data
# completeRecord <-rbind(transactions,t(diagnostics))
# return(completeRecord)
# case for overall wealth-split trajectories
return(diagnostics)
}Simulation Studies
A simple single case run can be setup very easily [in this case with no wealth adjustment).
# SIMPLE DIAGNOSTIC CASE :: SINGLE RUN
# save to object
output<-stepper(nsteps = 10000,agents = 200,rate = 0)
plot(output[,4],type="l",
main="Total Wealth of Top 1% Total versus the Bottom 50%",
ylab="Wealth Disparity (%)",
xlab="Interactions (n)")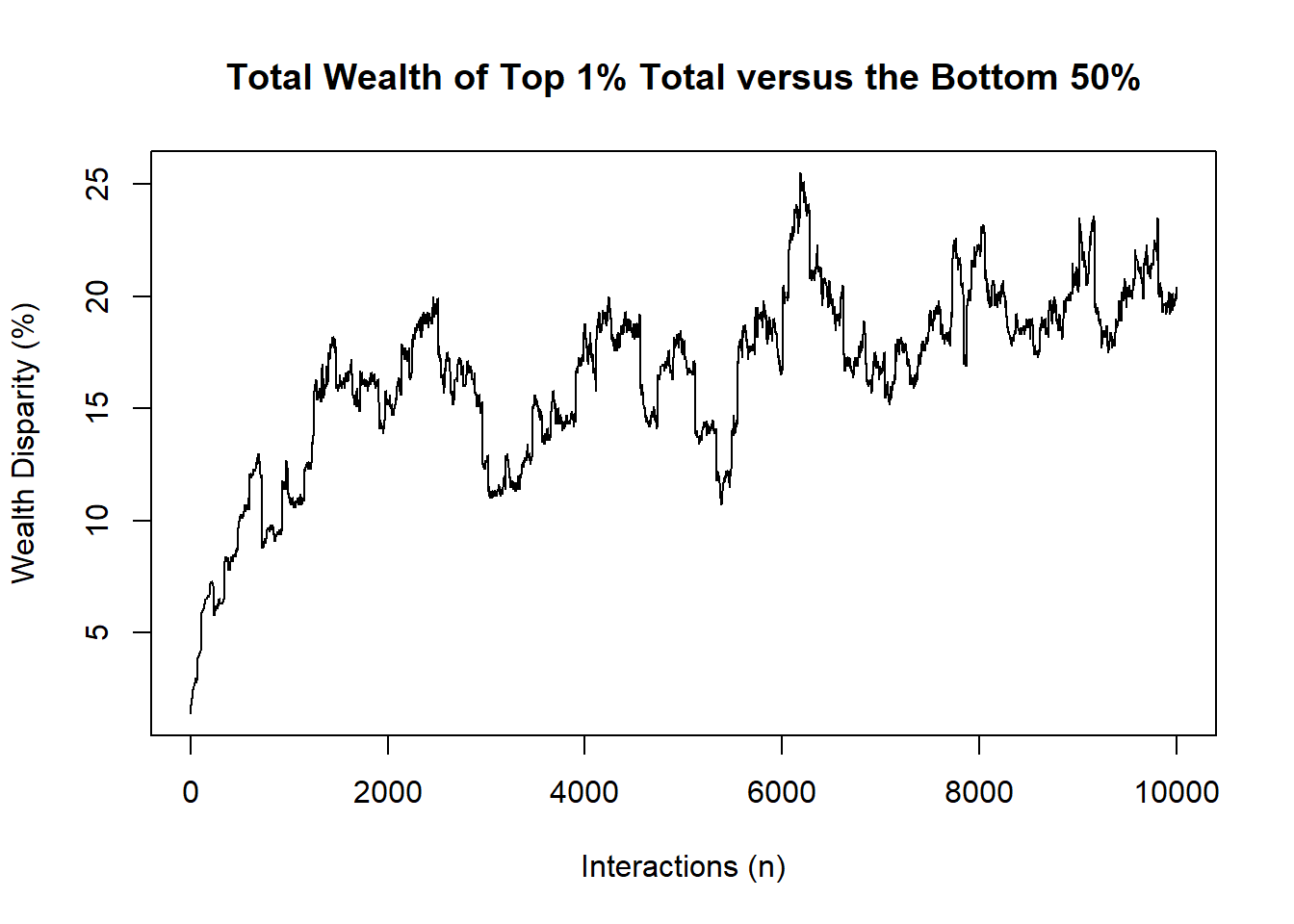
A multi-run case is setup as so:
# PRODUCTION CASE :: CARRY OUT MANY EXPERIMENTS
# repeating N times (100 is ~30mB)
reps <- 50
walks<-replicate(reps,stepper())
# get "average outcome"
avgOutcomes <-rowMeans(walks,dims=2)
plot(avgOutcomes[,4],type="l",
main="Total Wealth of Top 1% Total versus the Bottom 50%",
ylab="Wealth Disparity (%)",
xlab="Interactions (n)")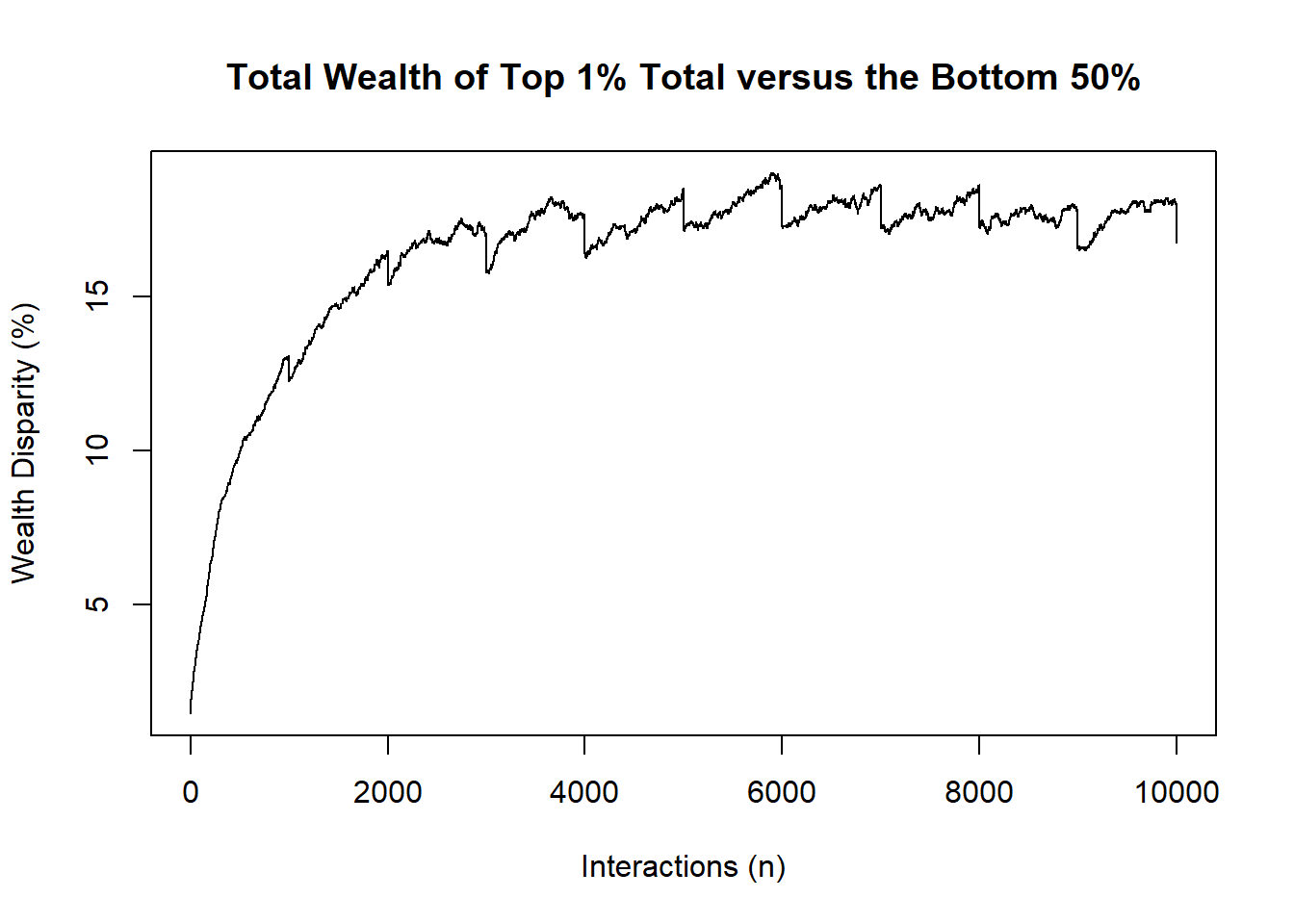
The above plot shows the mean trajectories of 50 simulations. Notice how the inequality gap is capped and readjusted via a “zigzag-pattern” when a wealth-redistribution scheme is applied.
replicate is a wrapper to the regular use of sapply for repeated evaluation of an expression (which will usually involve random number generation).↩